前言
近期在做推荐系统的时候再一次遇见了 word2vec,之前在学 nlp 的时候看过,不过看的比较快没有去深入研究其中的一些细节,到现在已经差不多了。这篇文章提出的 Embedding 对于 nlp 和 rec 的意义过于重大,趁着这两天公司事情不是很多,我打算来好好精读一下 word2vec 的系列文章。
word2vec 系列作品简介
word2vec 最早在 2013 年由 Tomas Mikolov 在《Efficient Estimation of Word
Representations in Vector
Space》中提出,后续还有两篇工作更加完善地进行了阐释。我把这三篇文章链接放在下面,大家可以按照顺序进行阅读。
Mikolov 的开山之作(2013 年第一篇) 《Efficient Estimation of Word
Representations in Vector Space》
首次提出了 word2vec 算法,包含两个模型:CBOW 和 skip-gram
对比了之前在语言表示的一些 work,比如 NNLM
Mikolov 的后续论文(2013 年第二篇) 《Distributed Representations of
Words and Phrases and their Compositionality》
这篇论文在 NeurIPS 2013 发表,是 Word2Vec
的第二篇论文,比第一篇更详细。
它引入了 负采样(Negative Sampling) 和 层次 Softmax(Hierarchical
Softmax) 等优化方法,并提供了更完整的训练目标函数描述
Rong (2014) 的详细推导论文 《word2vec Parameter Learning
Explained》(Xin Rong, 2014)
这是对 Word2Vec 数学原理最完整的解释之一,涵盖了: - Skip-gram 和
CBOW 的 损失函数推导 - 原始 Softmax 的梯度计算 - 负采样(NEG)和层次
Softmax(HS)的优化方法 - 训练过程的详细数学分析
什么是词向量
计算机是无法理解我们的自然语言的,想让计算机理解自然语言就要对齐进行编码。一种常见的编码手段就是独热编码(one-hot) 。但是这种编码的维度非常高并且很稀疏,任意两个向量之间还都是正交的,因此无法捕获两个词语的相关性特征。如果有一种方法能够将其映射到一系列低维稠密向量,机器就可以很好的学习不同词语之间的关系,比如:丈夫 - 妻子 + 国王 = 王后” 这样的关系。这就是词向量(Embedding)
的由来,其中产生词向量最经典的模型就是 word2vec
word2vec 的基本框架
word2vec 是 Google 研究团队里的 Tomas Mikolov 等人于 2013 年的《Efficient
Estimation of Word Representations in Vector
Space》以及后续的《《Distributed Representations ofWords and Phrases and
their
Compositionality》两篇文章中提出的一种高效训练词向量的方法,包含 Continuous
Bag-of-Words Model (CBOW) 和 Continuous Skip-gram
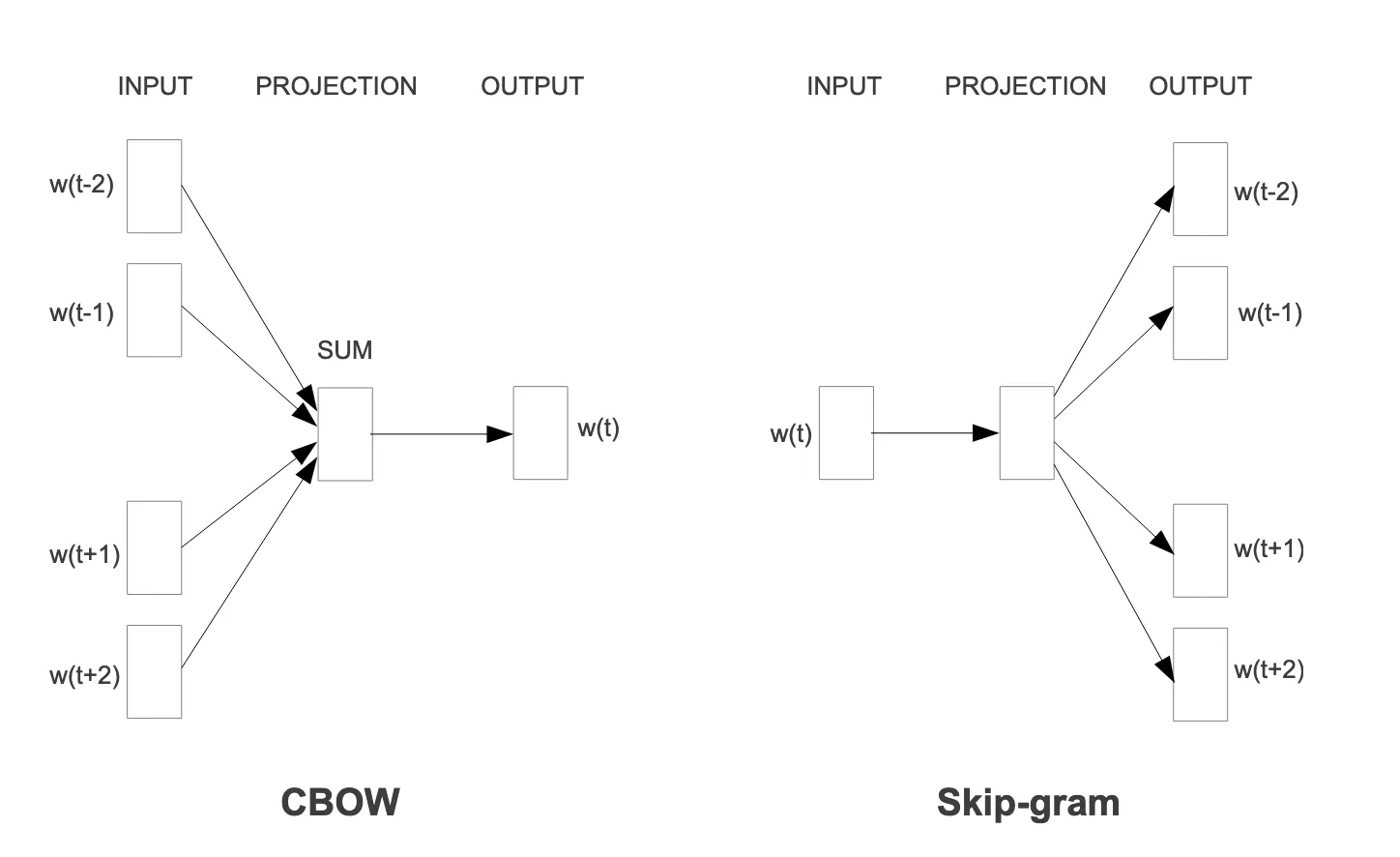
Model (skip-gram) 两个模型
alt text
其中,CBOW 模型是给定一个词的上下文词,希望预测这个词;而 skip-gram 是给定一个词,希望预测它的上下文词
跳元模型(Skip-Gram)
1)Skil-gram 语料构建
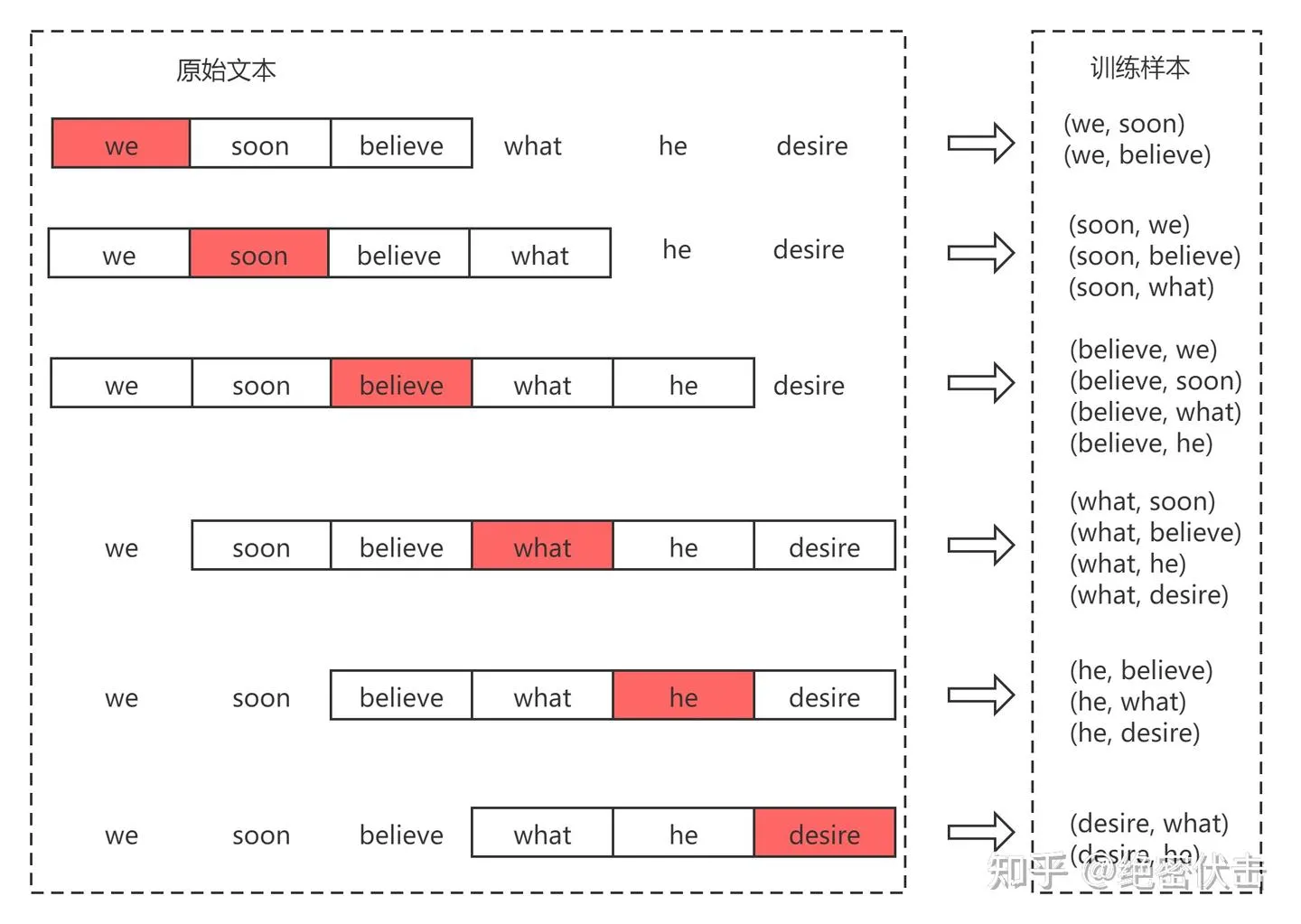
以 “we soon believe what he desire” 为例,滑动窗口大小
alt text
Skip-gram 是一个多分类的模型,当中心词是 believe 时,应该使得” We”,“soon”,“what”,“he” 出现概率最大,即
假设上下文词是在给定中心词的情况下独立生成的(即条件独立性)。在这种情况下,上述条件概率可以重写为:
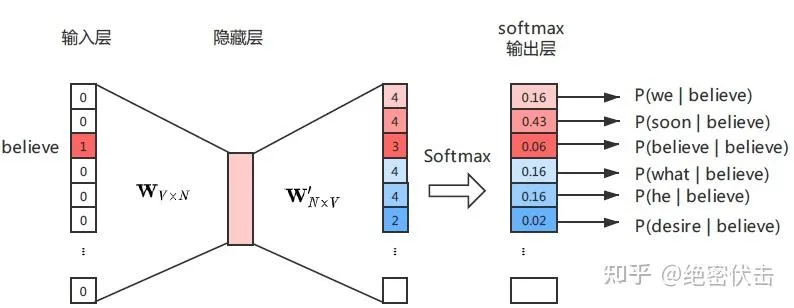
2)Skip-gram 模型结构
下图是 Skip-gram 模型结构,输入词” believe” 先经过一个隐藏层,得到其隐向量
alt text
根据上图的模型结构,我们可以得出,给定输入词
定义条件概率: 给定中心词 (w_c
),其上下文窗口内的某个词 (w_o) 的条件概率由 softmax
计算:
其中: - Missing superscript or subscript argument _c^ 行 )。 - 列 )。 -
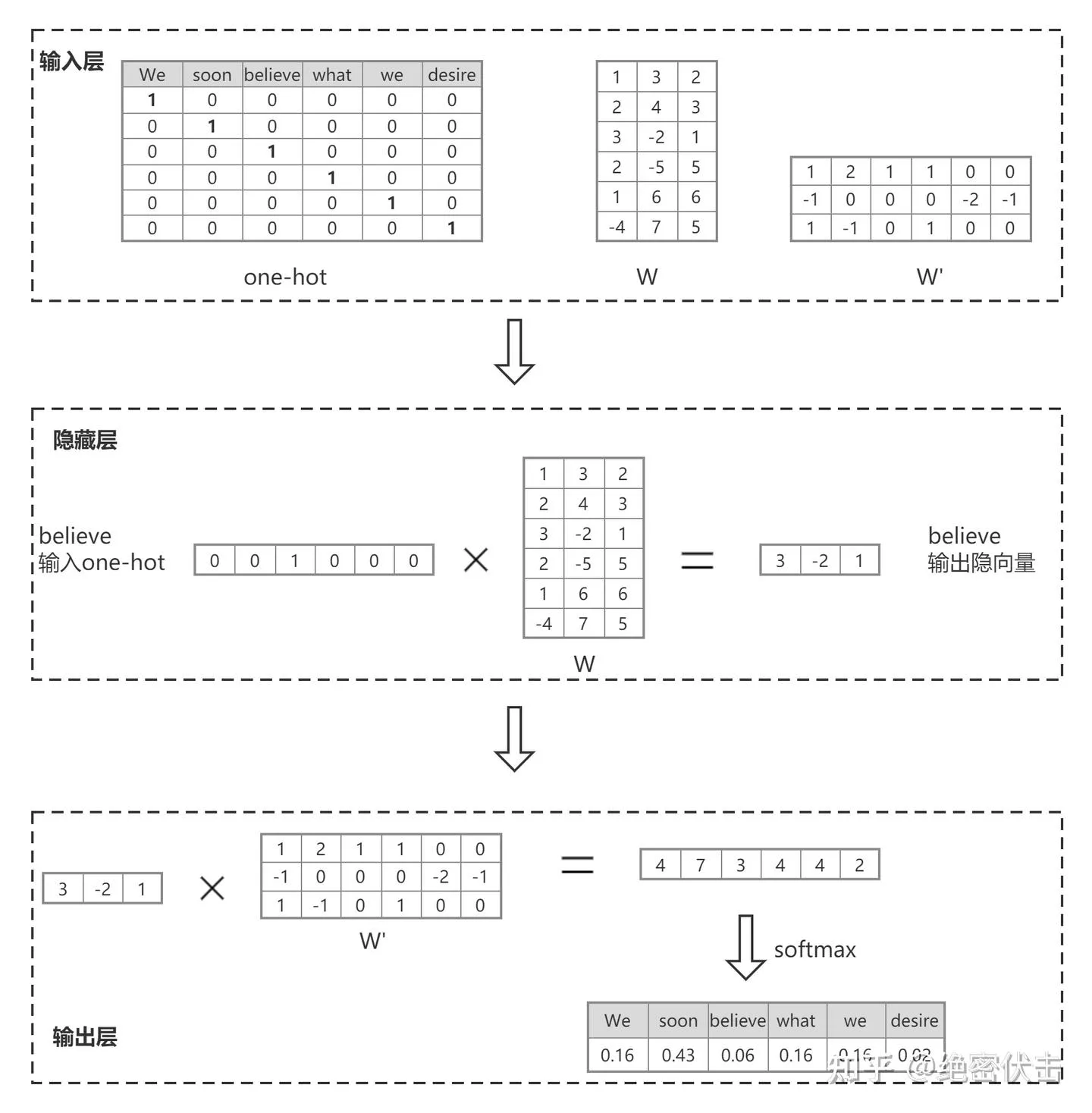
这里举一个例子说明上图模型结构是如何根据输入词
alt text
3)Skip-gram 模型训练
Skip-gram
的目标是最大化所有训练样本(中心词 - 上下文词对)的联合概率 。假设语料库有
(T) 个词,窗口大小为 (m),则每个中心词 (w_t) 对应 (2m)
个上下文词,其似然函数 为:
为了简化计算,我们通常取对数,得到对数似然函数 :
损失函数(Loss Function)
由于优化问题通常转化为最小化损失函数 ,我们对对数似然取负,得到负对数似然损失(Negative
Log-Likelihood, NLL) : [ () = - {t=1}^T {-m j m, j}
P (w_{t + j} | w_t) ] 其中: - () 是为了归一化,使损失与语料库大小无关。 -
最小化 ( () ) 等价于最大化 ( () )。
计算梯度(以原始 softmax 为例)
为了优化损失函数,我们需要计算梯度。以单个中心词 - 上下文词对 ( (w_c, w_o)
) 为例: [ {c,o}() = -P (w_o | w_c) = -() ] 展开后: [ {c,o}()
= -’_o c + ( {i=1}^V (’_i _c) ) ]
** 对中心词向量 (_c) 的梯度 ** [ = -‘o + {i = 1}^V P (w_i |
w_c) ’_i ] 其中: - ( -‘o ) 是正样本(真实上下文词)的梯度。 - (
{i = 1}^V P (w_i | w_c) ’_i )
是所有可能上下文词的期望梯度(负样本贡献)。
** 对上下文词向量 (’_o) 的梯度 ** [= -_c + P (w_o | w_c) _c]
4)优化改进:负采样(Negative
Sampling)
由于原始 softmax 计算复杂度高(( O (V) )),Word2Vec 采用
负采样(NEG) 近似优化: [ _{c,o}() = -(’_o c) -
{k = 1}^K (-’_k _c) ] 其中: - ( (x) = ) 是 sigmoid 函数。 - (K)
是负样本数量(通常 (K = 5 20))。 - 负样本 (w_k) 从噪声分布 ( P_n (w) )
中采样(如 ( P_n (w) (w)^{3 / 4} ))。
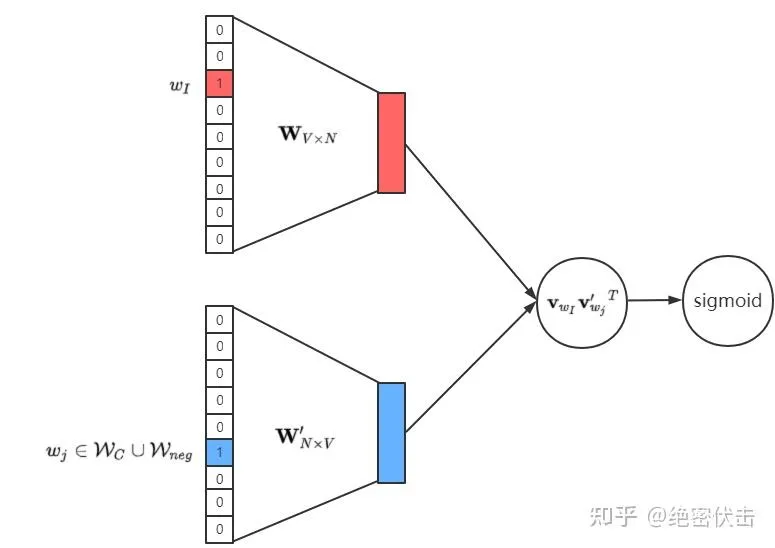
相比于原来需要计算所有词的预测误差,负采样方法只需要对采样出的几个负样本计算预测误差。这样一来,Skip-gram 模型的优化目标从一个多分类问题转化为一个近似二分类问题,模型结构变成如图的形式。
负采样把” 从海量词汇中选最合适的词” 的多分类问题,转化为” 判断当前词对是否合理” 的二分类问题。这类似于:
原始问题:“这些 10000 个选项中哪个是正确的?”
负采样:“我告诉你 1 个正确选项和 5 个错误选项,请学会区分它们”
alt text
梯度计算(负采样版) : [ = ( (’_o _c) - 1 ) ‘o +
{k=1}^K (’_k _c) ’_k ]
总结
概念
公式
条件概率 ( P(w_o | w_c) = )
似然函数 ( () = {t=1}^T {-m j m} P(w_{t+j} | w_t) )
损失函数 ( () = - {t=1}^T {-m j m} P(w_{t+j} | w_t) )
负采样损失 ( _{c,o}() = -(’_o c) - {k=1}^K (-’_k _c) )
核心思想 :
参考资料
https://blog.csdn.net/v_JULY_v/article/details/102708459
https://zhuanlan.zhihu.com/p/352169069